Objets connectés et suivi à domicile de patients traités pour un cancer

Le projet

Analyse de séries temporelles

Descripteurs statistiques Dynamic Time Warping Entropie Analyse de la première phase du traitement Références

Descripteurs statistiques

Pour caractériser nos signaux, nous nous sommes intéressés au descripteurs statistiques d'ordre 1, 2, 3 et 4 : moyenne, écart-type, asymétrie (skewness) et aplatissement (kurtosis). Ces deux derniers ordres vont nous permettre d'avoir l'information sur la forme de la série temporelle. Ces quatres paramètres consitituent un vecteur de caratérisation (feature vector) pour chaque signal. C'est sur ces vecteurs que nous allons pouvoir appliquer des algortihmes de clustering.

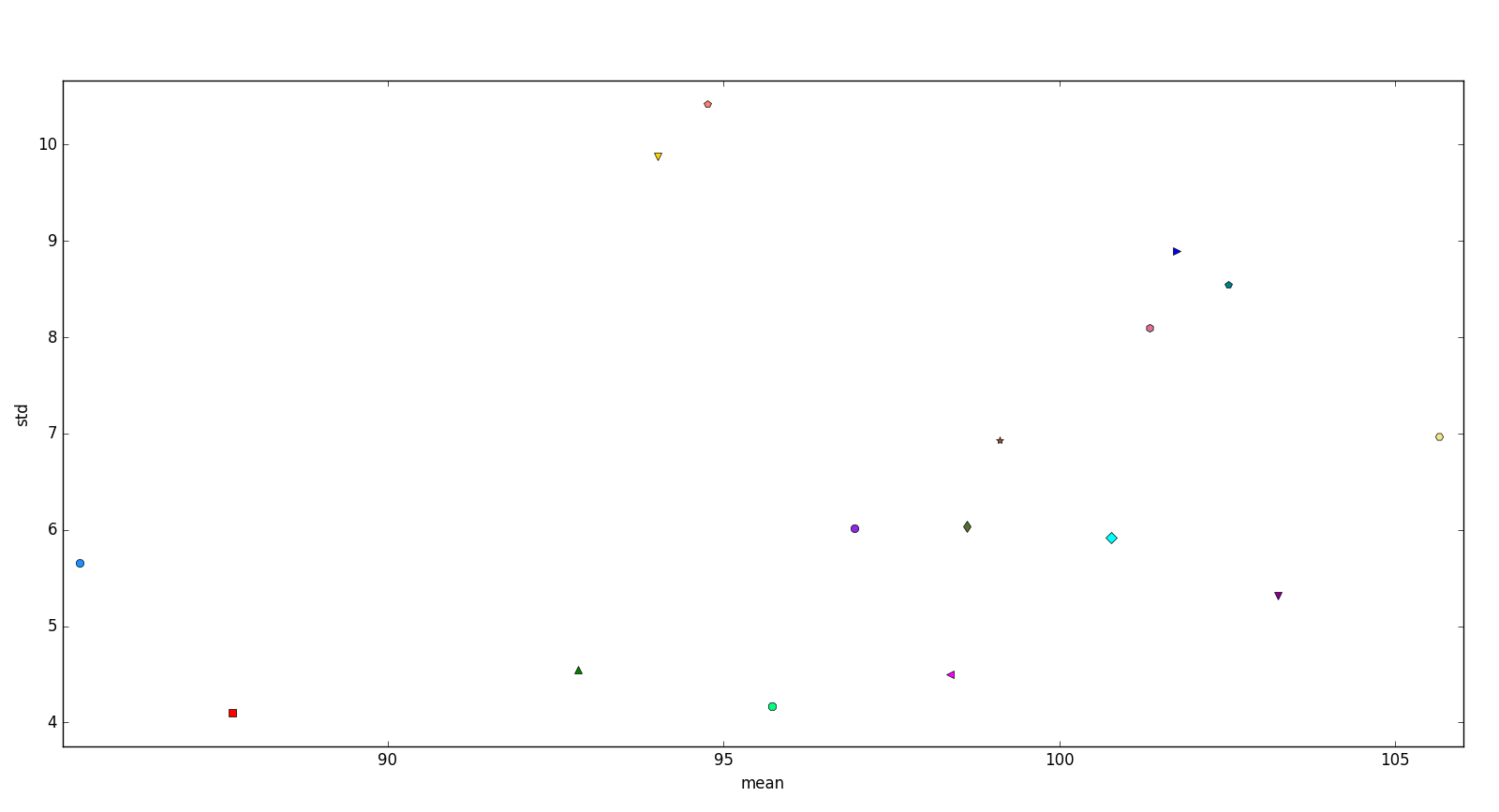
La figure suivante nous présente les descripteurs statistiques d'ordre 1 et 2 pour chaque patient.

représentation 2D des descripteurs statistiques d'ordre 3 (en abscisse) et 4 (en ordonnée)

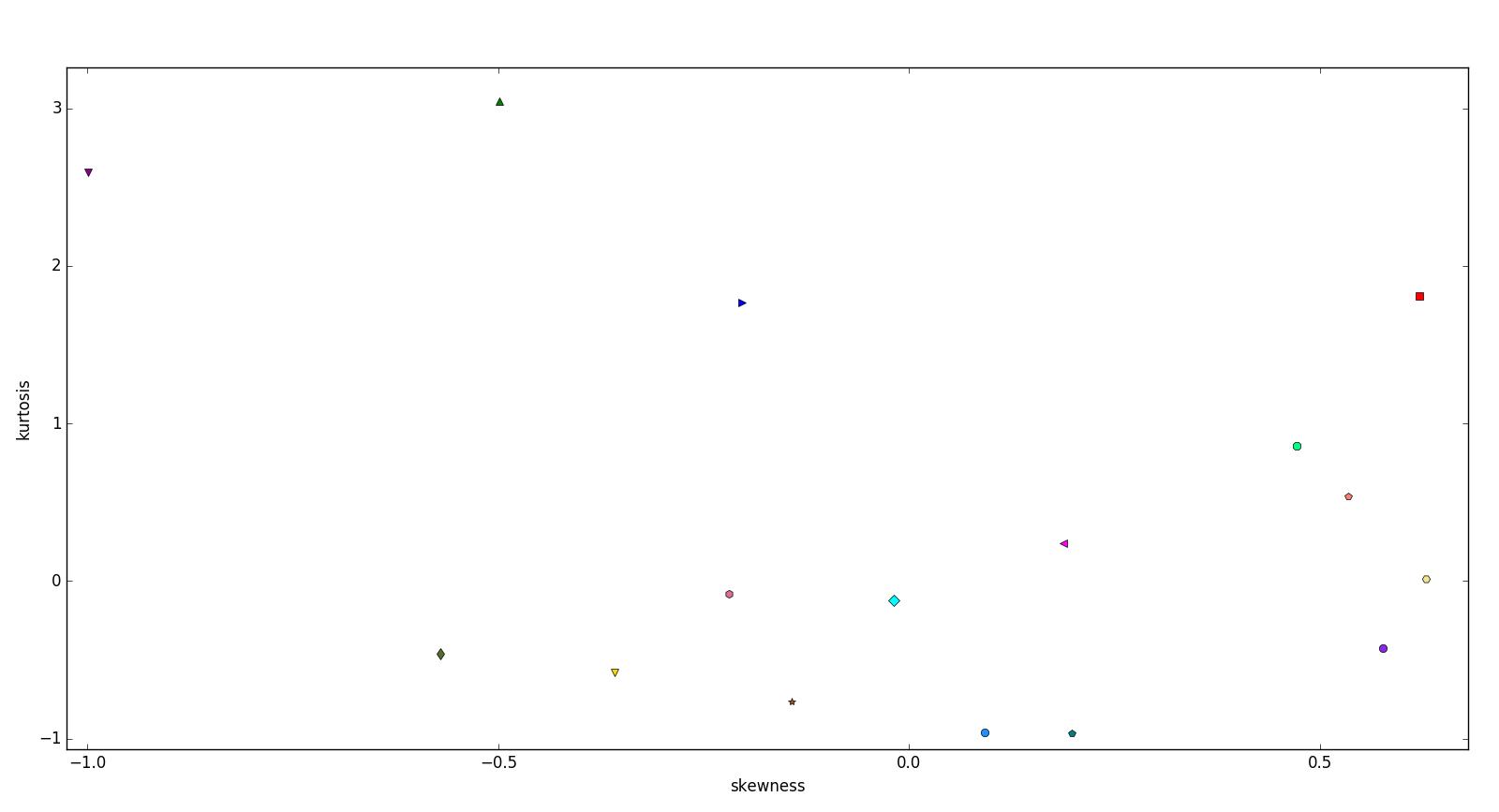
La figure suivante nous présente les descripteurs statistiques d'ordre 3 et 4 pour chaque patient.

La valeur moyenne de la pression artérielle varie d'un individu à l'autre, c'est pourquoi dans un premier temps nous avons décidé de créer un vecteur de caractérisation 3-dimensions avec pour chaque individu l'écart-type, l'asymétrie et l'aplatissement de sa PAM.

représentation 3D des descripteurs statistiques d'ordre 2 (en x) et 3 (en y) et 4 (en z)

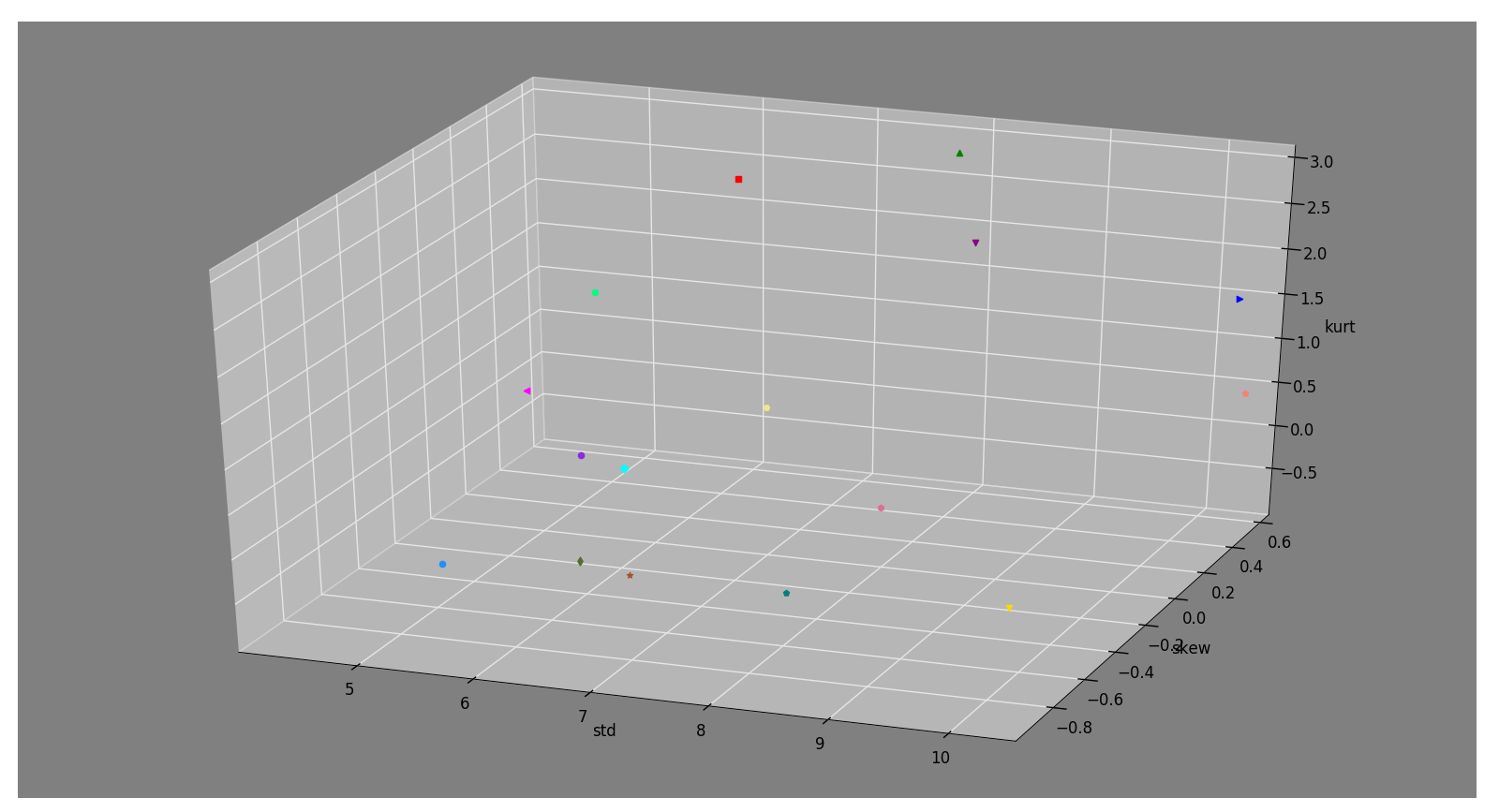
La figure suivante montre la représentation de ces vecteurs 3-D de caractérisation.

Nous avons également, pour voir l'intérêt des 4 descripteurs statistiques (présentés ci-dessus), créé un vecteur de caractérisation 4-dimensions avec pour chaque individu l'asymétrie, l'aplatissement, l'écart-type et la moyenne de sa PAM.

Dynamic Time Warping

Méthode Clustering hiérarchique Approximation linéaire par morceaux

Méthode

L'algorithme du Dynamic Time Warping permet de faire une mesure de distance entre deux signaux. Cette mesure considère le temps comme non linéaire et élastique ce qui permet d'obtenir un calcul de distance des signaux prenant en compte leurs décalages temporels.

Dans notre cas il est important de prendre en compte ce décalage temporel car la réaction au traitement n'est temporairement pas la même pour chaque patient. Par exemple, deux patients réagissant bien au traitement vont avoir une PAM qui augmente cependant, il peut y avoir un décalage de quelques jours entre ces deux patients ce qui montre l'intérêt d'utiliser une mesure de distance qui prend en compte ces décalages.

La valeur moyenne de la pression artérielle varie d'un individu à l'autre, c'est pourquoi nous devons normaliser nos signaux pour ne prendre en compte que les variations.

La notion de prise en compte des décalages temporels est illustrée dans la partie Illustrations pédagogiques -- Mesure de distance qui montre la différence entre la distance euclidienne (ne prenant pas en compte le décalage) et la DTW.

Clustering hiérarchique

Le clustering hiérarchique consiste à construire une suite de clusters emboîtés les uns dans les autres. Ces clusters seront donc mis en lien par le biais d'un arbre appelé également dendrogramme. Cette technique est très utile lorsqu'on ne connait pas à l'avance le nombre de cluster que nous cherchons. Pour construire ce dendrogramme, il nous faut choisir une mesure de distance (euclidienne, DTW, ...) et un critère d'agrégation (lien minimum, maximum ou moyen).

illustration qui montre la construction d'un dendrogramme dans le cas d'un clustering hierarchique ascendant

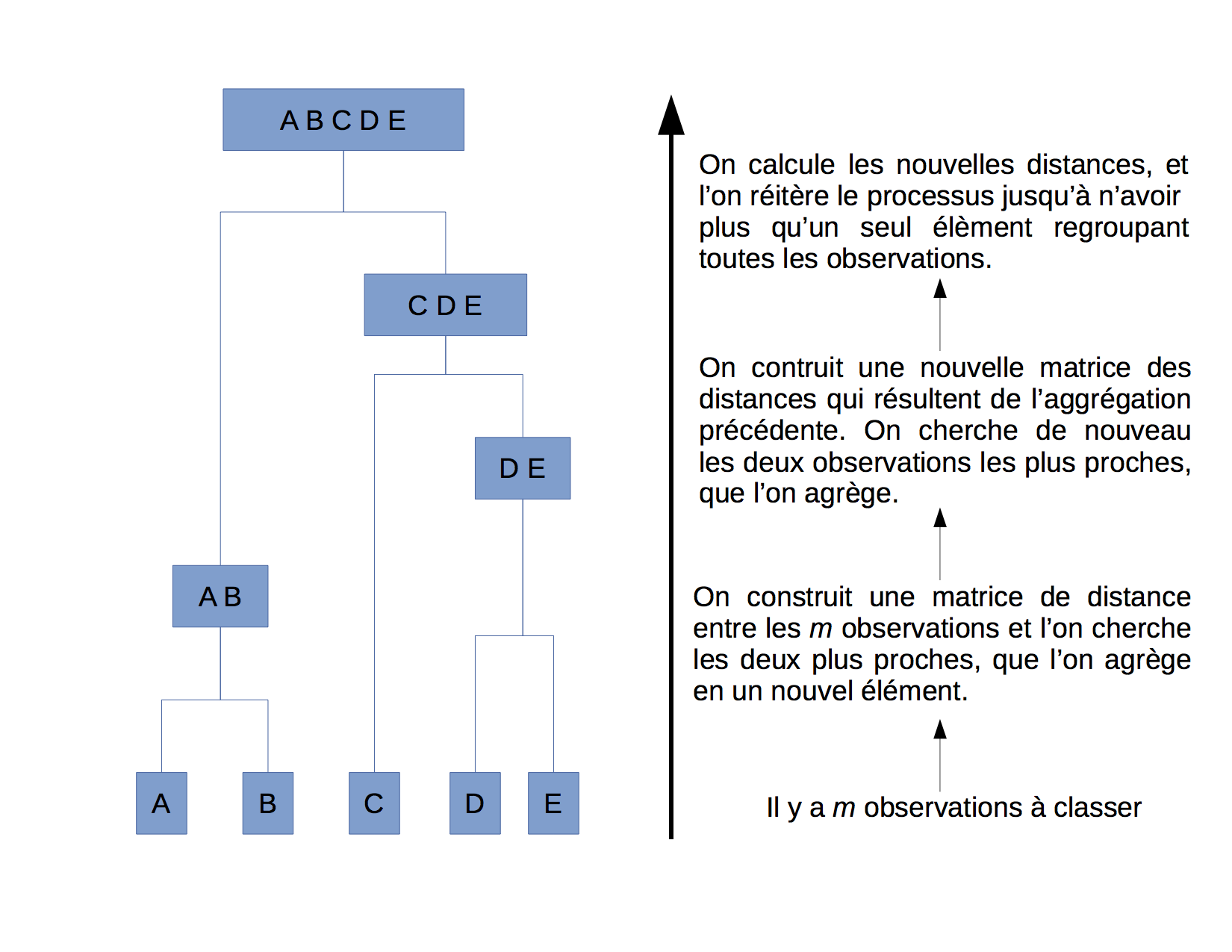
La figure suivante illustre la construction d'un arbre dans le cas d'un clustering hiérarchique ascendant.

A l'aide de la DTW, nous avons pu obtenir une matrice de distance. Cette matrice représente la distance entre chaque signal de la PAM pour chaque patient.

Pour le clustering hiérarchique appliqué à nos données, nous avons choisi d'utiliser la DTW comme mesure de dissimilarité. Pour regrouper les patients à l'aide de la matrice de distance nous avons choisi le critère du lien moyen qui utilise la moyenne des distances entre les éléments de chaque classe pour effectuer les regroupements.

dendrogramme obtenu pour tout nos patients avec seuil fixé pour avoir 3 groupes

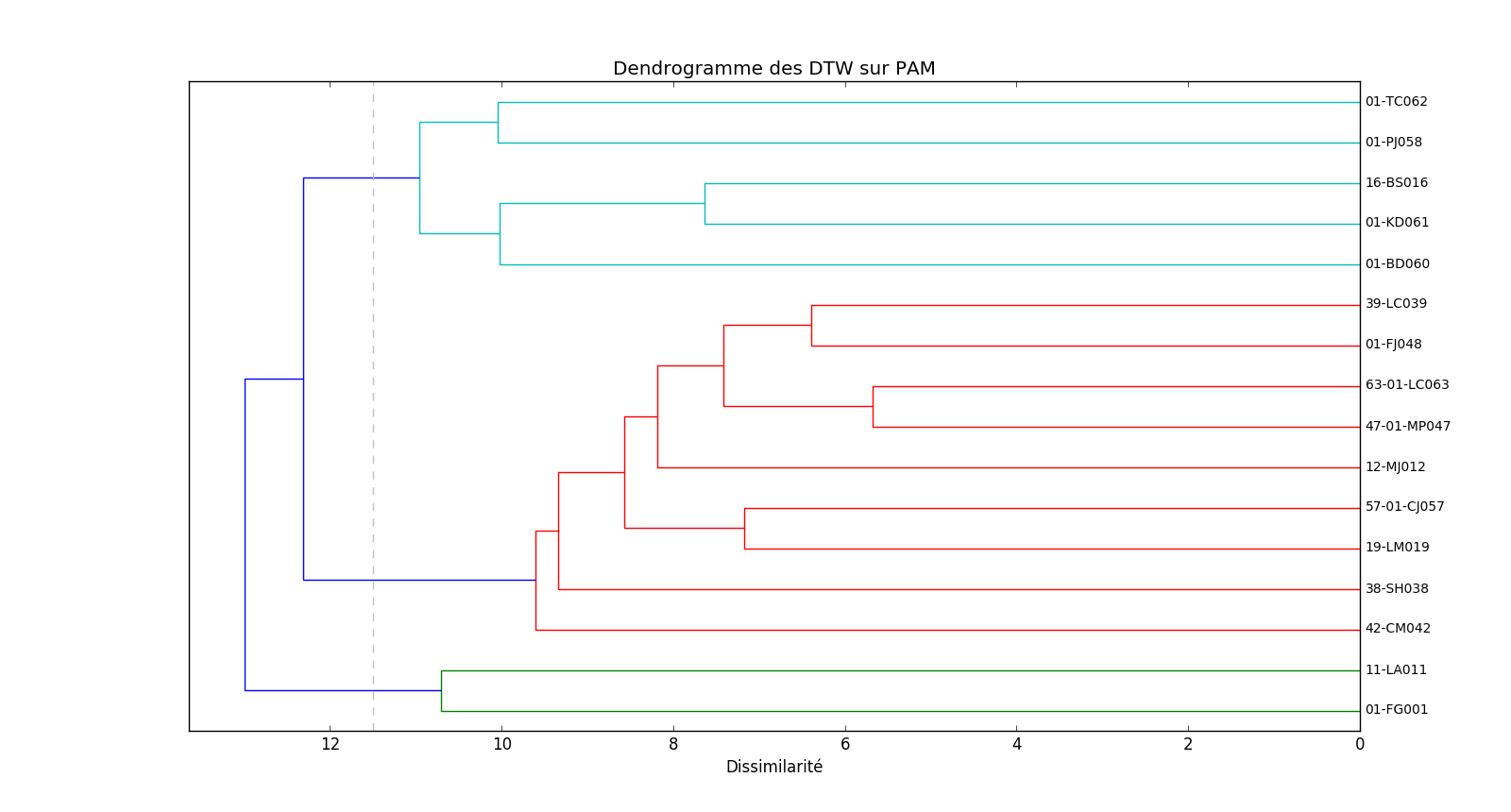
La figure suivante nous montre le dendrogramme obtenu.

Approximation linéaire par morceaux

L'approximation linéaire par morceaux -- \emph{Piecewise Linear Representation (PLA)} -- consiste à représenter un signal par un ensemble de segments. Le nombre de segments varie en fonction du signal car il dépend uniquement d'une marge d'erreur fixée au préalable. Cette technique nous permet de filtrer le bruit (variations très court terme et non significatives) des signaux.

Il existe trois algorithmes de PLA : sliding window, top-down et bottom-up. Après visualisation des trois algorithmes sur nos données, nous avons choisi d'utiliser l'algorithme sliding window avec une marge d'erreur égale à 7.

Dans un premier temps, nous avons appliqué cette méthode sur nos signaux normalisés. Dans un second temps, nous avons appliqué un clustering hiérarchique à ces nouveaux signaux pour obtenir un dendrogramme.

visualisation du rendu de la PLA sur 3 signaux de la PAM de nos patients

Exemples de la PLA obtenue sur trois signaux.

dendrogramme obtenu pour tous les signaux après PLA de nos patients avec seuil fixé pour avoir 3 groupes

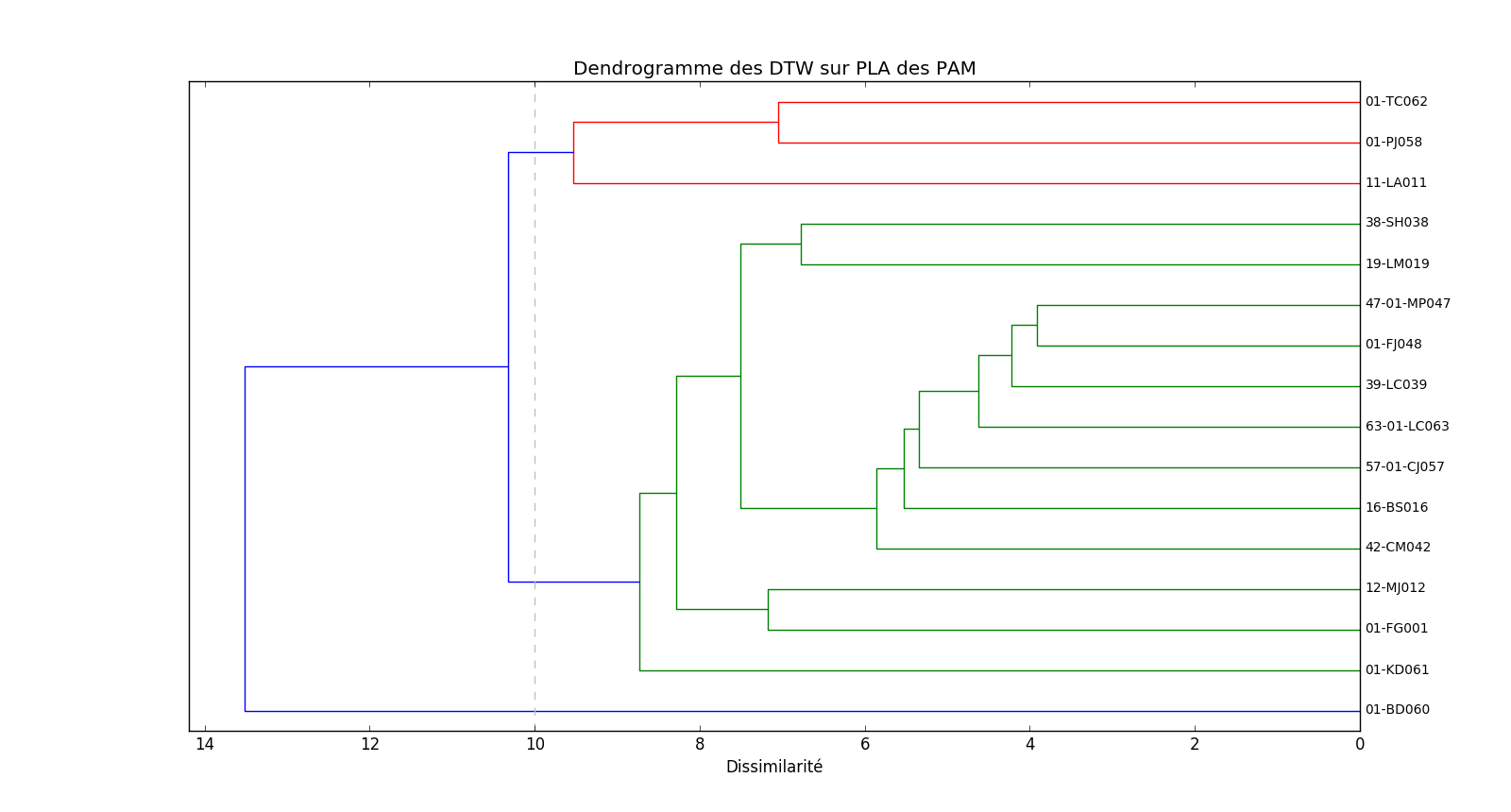
La figure suivante nous montre le dendrogramme obtenu.

Entropie

Entropie de l'échantillon Entropie mutli-échelle Refined Composite Multiscale Entropy Entropie de l'échantillon croisée

Entropie de l'échantillon

L’entropie d’échantillon (Sample Entropy) caractérise la quantité d’information apportée par un signal échantillonné. Elle est calculée à partir de l’équation ci-dessous. Plus l'échantillon est incertain (irrégulier) alors plus il apporte d'information donc plus son entropie sera élevée. Il est également intéressant, en traitement du signal, de connaitre la complexité d'un signal, par exemple un signal bruit-blanc (white noise) est très irrégulier cependant comme il n'est que composé de répétitions régulières sa complexité est faible. Donc ce type de signal a une entropie élevée et pourtant une complexité faible, c'est pourquoi nous devons nous intéresser à l'entropie multi-échelle (Multiscale Entropy).

SampEn(m,r,N)=-\ln\frac{A^m(r)}{B^m(r)}

Avec $r$ la tolérance, $m$ la longueur du modèle, $A^m(r)$ la probabilité que deux séquences correspondent pour $m+1$ points et $B^m(r)$ la probabilité que deux séquences correspondent pour $m$ points.

Entropie mutli-échelle

L'entropie multi-échelle (MSE) est une méthode qui permet de mesurer la complexité d'une série temporelle, en calculant son irrégularitée sur plusieurs échelles. Cette méthode est appropriée au traitement de signaux physiologiques.

La MSE consiste à calculer l'entropie de l'échantillon, pour chaque échelle d'un signal en grain grossier (coarse graining) obtenu à l'aide de l'équation ci-dessous.

y_j^{(\tau)}=\frac{1}{\tau}\sum_{i=(j-1)\tau+1}^{j\tau}x_i

Avec $\tau$ le facteur d'échelle et $1\leqslant j\leqslant \frac{N}{\tau}$ .

Cette méthode nous permettra de savoir quelle est la quantité d'information apportée par notre signal sur chaque échelle. Par exemple si notre signal chute l'échelle 4 nous savons que cette échelle n'apporte pas d'information supplémentaire.

L'entropie multi-échelle basique admet tout de même un défaut c'est qu'elle n'est pas adaptée aux séries temporelles courtes, c'est pourquoi nous avons dû nous intéresser à la Refined Composite Multiscale Entropy (RCMSE).

Refined Composite Multiscale Entropy

Le calcul de la MSE génère des valeurs indéfinies pour les séries temporelles courtes. Quand nous utilisons les grandes échelles temporelles $\tau$ , la série temporelle en grain-grossier admet un nombre très faible d'échantillon cela peut donc conduire à des mesures d'entropie de l'échantillon indéfinies. C'est pourquoi la refined composite multiscale entropy (RCMSE) a été introduite.

Dans la mesure de la RCMSE, la série temporelle en grain-grossier $y_k^{(\tau )}$ est obtenue pour différentes valeur de $k$ :

y_{k,j}^{(\tau)}=\frac{1}{\tau}\sum_{i=(j-1)\tau+k}^{j\tau+k-1}x_i

Avec $\tau$ le facteur d'échelle, $x$ le signal original, $1\leqslant j\leqslant \frac{N}{\tau}$ et $1\leqslant k\leqslant\tau$ .

La mesure de la RCMSE à l'échelle $\tau$ est calculée à l'aide de l'équation suivante :

RCMSE(x,\tau,m,r)=-\ln\frac{\sum_{k=1}^\tau n_{k,\tau}^{m+1}}{\sum_{k=1}^\tau n_{k,\tau}^{m}}

Avec $r$ la tolérance, $m$ la taille de l'échantillon, $n_{k,\tau}^{m+1}$ et $n_{k,\tau}^{m}$ sont les nombre de correspondance pour chaque $\tau$ du signal en grain-grossier pour, respectivement, $m+1$ et $m$ .

Pour caractériser cette mesure, nous avons choisis deux descripteurs, le premier est l'indice de complexité qui est calculé en faisant la somme des entropies des échantillons pour chaque échelle temporelle $\tau$ . Il permet de connaitre le niveau de complexité de chaque signal. Le second est l'allure de chaque courbe qui permet de comparer l'évolution de l'information apportée par chaque signal à différentes échelles temporelles.

Il est recommandé que la taille de l'échantillon pour calculer la RCMSE soit comprise entre $10^m$ et $20^m$ . Nos données ont 63 échantillons. Nous avons donc choisi $m=1$ et $\tau\leqslant 5$ . De plus, nous avons fixé $r=0,15\times \sigma$ (où $\sigma$ est l'écart-type de la série temporelle à l'échelle $\tau =1$ ).

Après visualisation des courbes de RCMSE de la PAM de chaque patient, nous avons observé 3 types d'allures différents : les courbes globalement décroissantes (cluster 1), les courbes globalement croissantes (cluster 2) et celles qui admettent des valeur d'entropie d'echantillon non-monotone (cluster 3).

résultat du clustering sur l'allure des courbes de RCMSE illustrant chaque courbe de RCMSE dans une fenêtre de son cluster

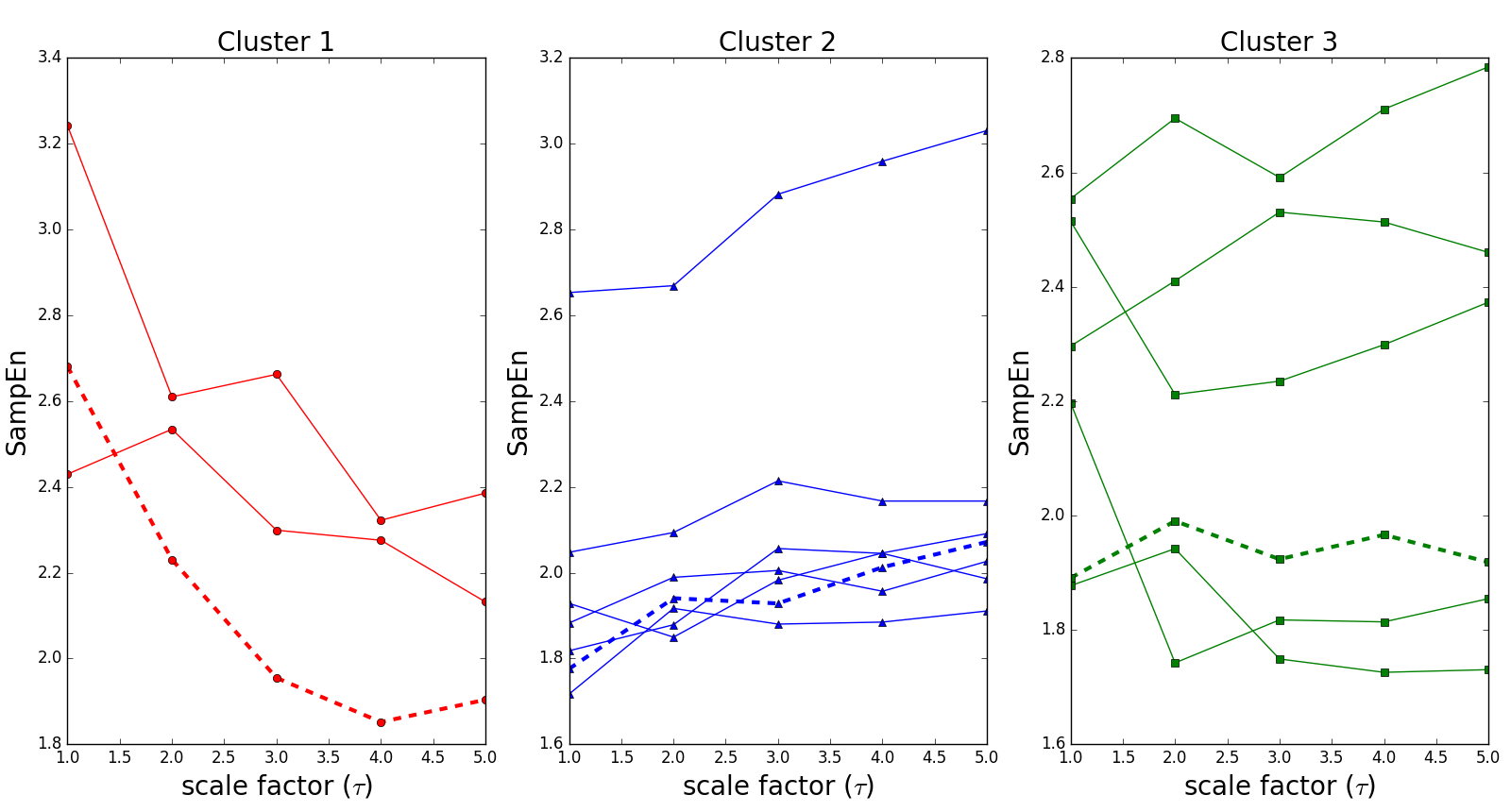
La figure suivante montre le résultat du clustering des courbes de RCMSE des 16 patients.

figure représentant la courbe de RCMSE des trois signaux de référence vu dans la figure ci-dessus

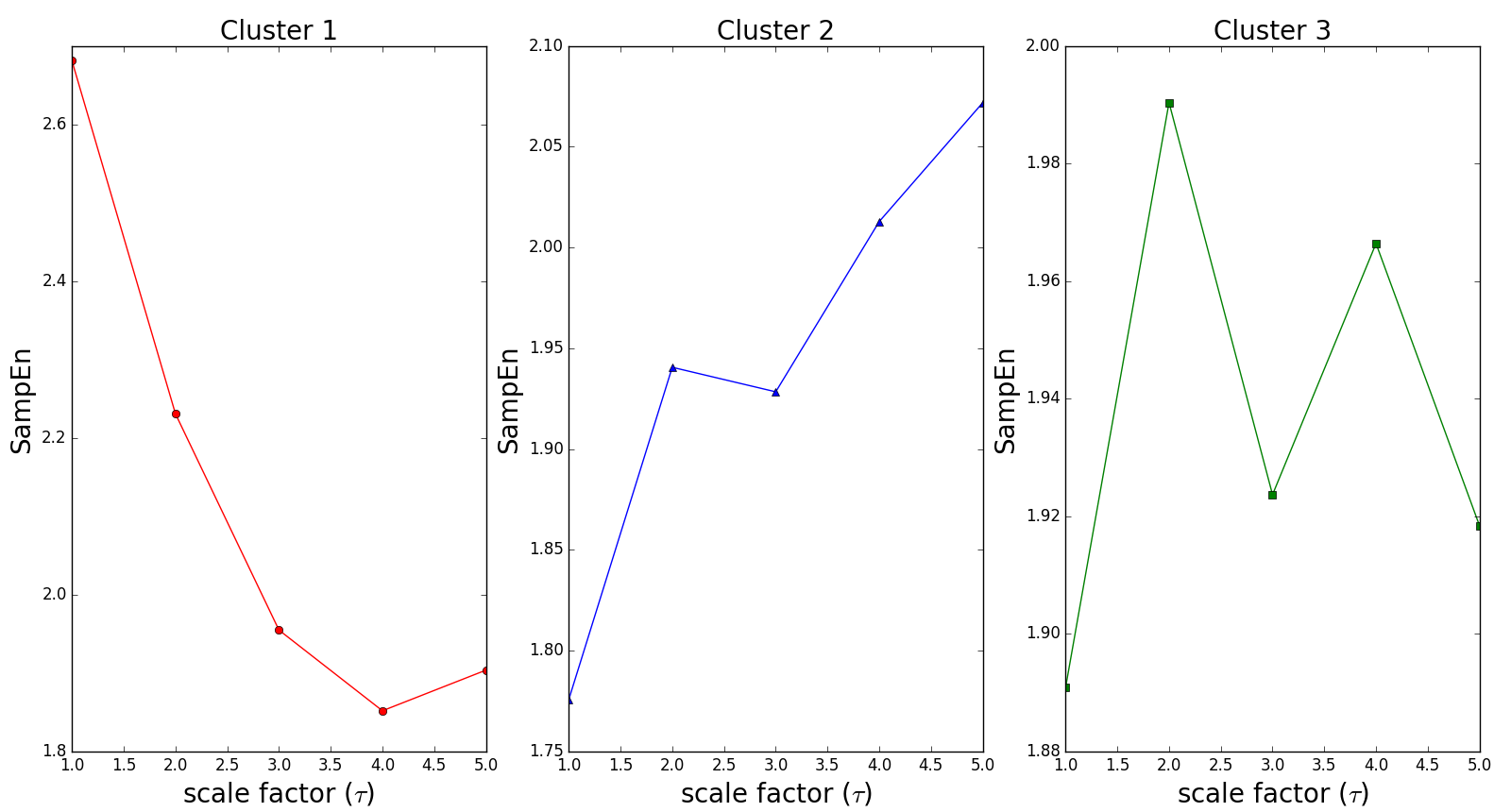
La figure suivante montre la forme de la courbe de RCMSE pour chaque signal de référence.

Nous avons également regroupé nos patients par le biais de l'indice de complexité, obtenus sur la RCMSE de la PAM.

visualisation de tous les indices de complexité pour tout nos patients

La figure suivante l'indice de complexité obtenu pour chaque patient.

Entropie de l'échantillon croisée

L'entropie de l'échantillons croisée permet de mesurer l'asynchronisme entre deux signaux en utilisant l'entropie de l'échantillon. Pour calculer l'entropie de l'échantillon croisée il fait suivre l'algorithme suivant :

Nous avons dans notre cas décidé d'utiliser pour les 16 patients cette méthode sur nos deux signaux d'entrée la PAS et la PAD. Cette méthode est également adaptée aux séries temporelles courtes. Dans notre cas, la PAS et la PAD ne sont pas des signaux de même amplitude et de même ordre de grandeur c'est pourquoi nous avons dû normaliser ces signaux Le résultat de cette mesure sur nos patients est illustrée par la Figure ci-dessous :

visualisation de l'entropie de l'échantillon croisée de nos patients dans un espace 1-D

Analyse de la première phase du traitement

L'évolution de la tension pendant le traitement admet un profil qui a une première phase ascendante et une seconde décroissante. La première phase dure entre 14 et 21 jours et la seconde jusqu'à environ 30 jours. Par cette méthode, nous allons essayer de mettre en lien le nombre de dépassement des seuils de tension avec l'allure des courbes de la PAM.

Pour détecter le profil des patients nous avons approximé par une droite ( $y=ax+b$ ) la courbe de l'évolution de la PAM sur chacune des périodes ( $P1a$ [0 à 13 jours], $P1b$ [14 à 20 jours], $P1$ [0 à 20 jours], $P2$ [21 à 32 jours]).

Le premier objectif a été de savoir quelle période ( $P1a$ ou $P1$ ) nous devons prendre pour la première phase (ascendante). Nous avons mis au point l'algorithme ci-dessous. Nous rappelons tout d'abord que l'approximation se fait par l'équation d'une droite $y=ax+b$ donc $a$ nous donne le coefficient directeur de la droite et donc son allure (croissante ou décroissante).

algorithme expliquant comment savoir quelle période choisir pour la premiere phase

Ensuite nous avons calculé le taux de dépassement journalier qui revient à savoir sur combien de jours le patient a eu une PAS ou une PAD au dessus du seuil sur la première phase du traitement. Puis nous devons tracer le graphe représentant ce taux de dépassement en fonction de $a$ . Nous nous sommes arrêtés à 32 jours car c'est le nombre minimal d'échantillon des patients ayant un nombre d'échantillon supérieur à 30. Ce choix nous a permis d'inclure 7 nouveaux patients par rapport aux études précédentes.

Ce premier algorithme nous a fait ressortir 6 patients qui ne respectent pas le profil théorique. Ces patients sont donc situés à gauche de la ligne grise en pointillés sur la figure ci-dessous qui représente le taux de dépassement de chaque patient durant la première phase en fonction du coefficient directeur de cette première phase. Nous avons ajouté en annotation bleue le taux de dépassement de chaque patient pour la seconde phase.

figure représentation 2-D avec en abscisse le coefficient directeur de la première phase et en ordonnée le taux de dépassement de cette première phase

Nous pouvons constater que les patients qui se situent en bas du graphe ont majoritairement un taux de dépassement faible avant et après (groupe 1), et inversement pour ceux qui se situent en haut du graphe (taux de dépassement important avant et après (groupe 2)). Les figures ci-dessous nous montrent 3 signaux représentatifs de ces groupes.

représentation 2-D de la PAS (1 graphe) et de la PAD (1 autre graphe) des signaux du groupe 1

représentation 2-D de la PAS (1 graphe) et de la PAD (1 autre graphe) des signaux du groupe 2

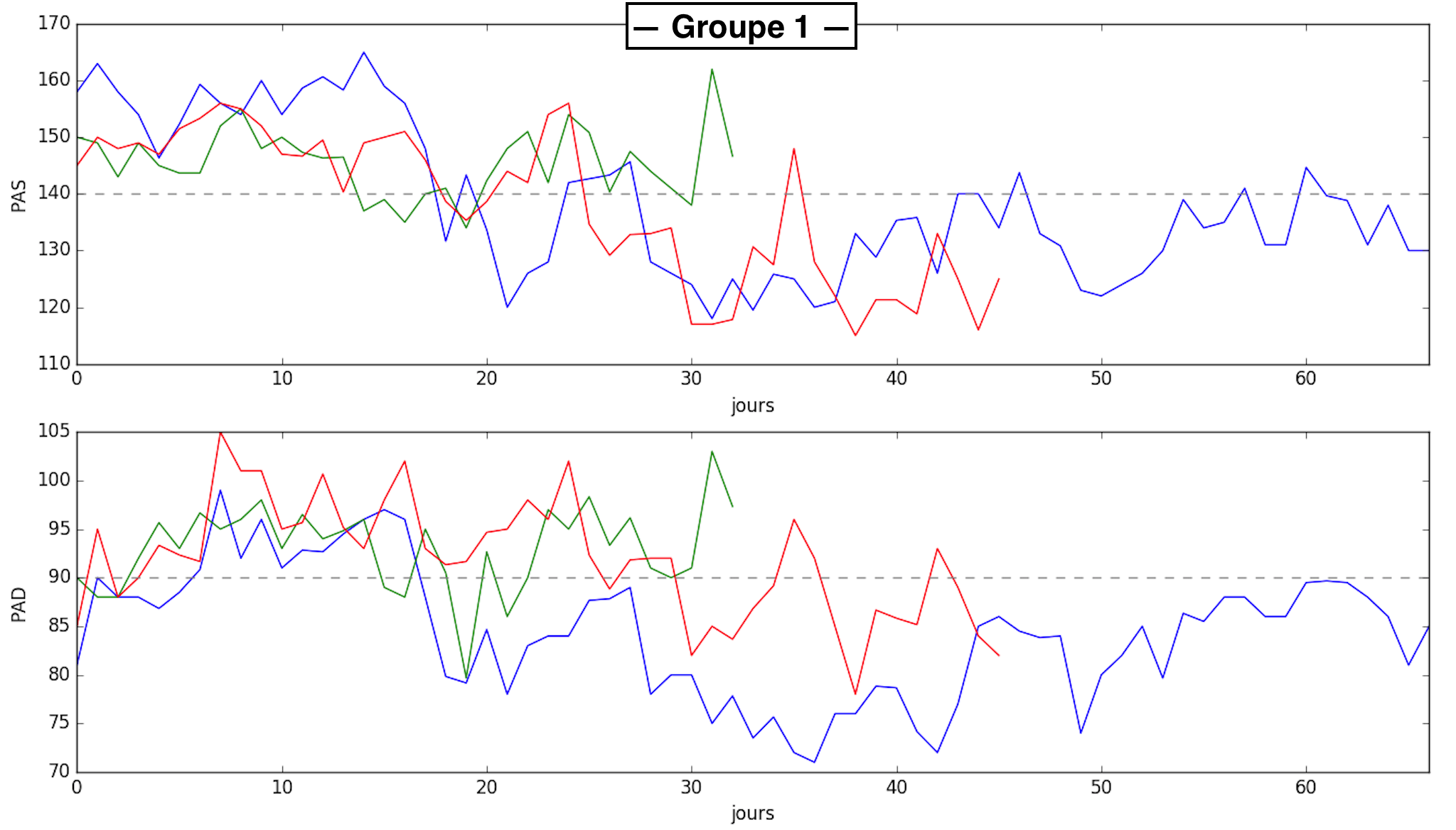
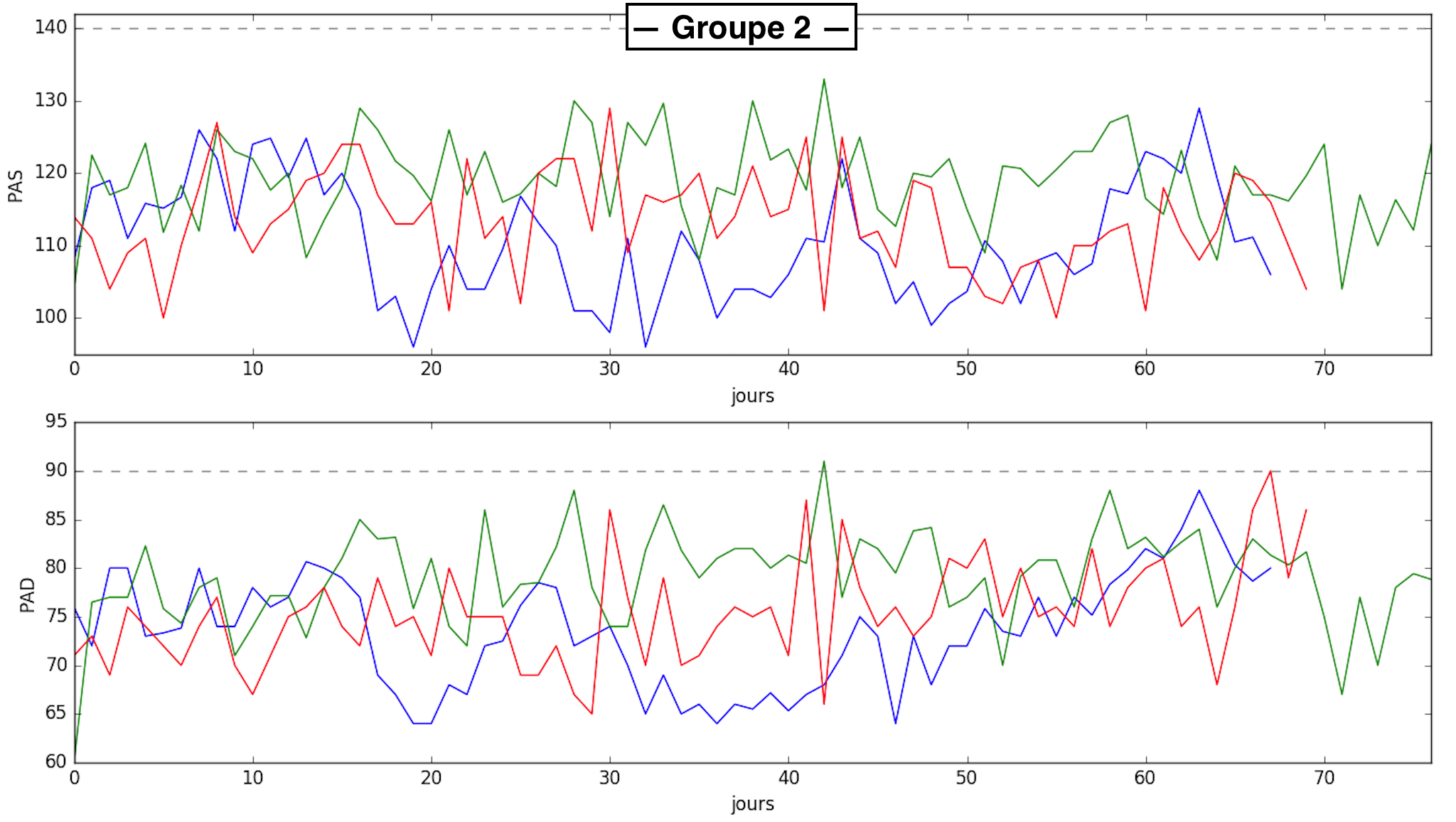
Nous avons tout de même des problèmes avec 2 patients (entourés en rouge) qui se trouvent en bas du graphe alors qu'ils ont un taux de dépassement qui augmente significativement entre la phase 1 et la phase 2. Nous avons également un autre patient qui pose problème (entouré en bleu) qui se trouve au milieu, voir plutôt haut, alors que son taux de dépassement diminue fortement. Pour les patients entourés en rouge, représentés en bleu et en rouge sur la figure ci-dessous, les profils sont vraiment différents car pour le bleu le taux de dépassement sur le long terme tend vers 0 alors que pour le rouge il est élevé. Il existe une différence dans le traitement de ces deux patients (prise ou non d'un anticoagulant), elle pourrait être une réponse à ce problème de classification. Pour le patient entouré en bleu, représenté en vert sur la figure ci-dessous, le profil montre que le taux de dépassement est élevé sur le long terme et donc rend cohérent sont placement dans l'espace caractéristique.

représentation 2-D de la PAS (1 graphe) et de la PAD (1 autre graphe) des signaux du groupe des patients qui nous posent problème

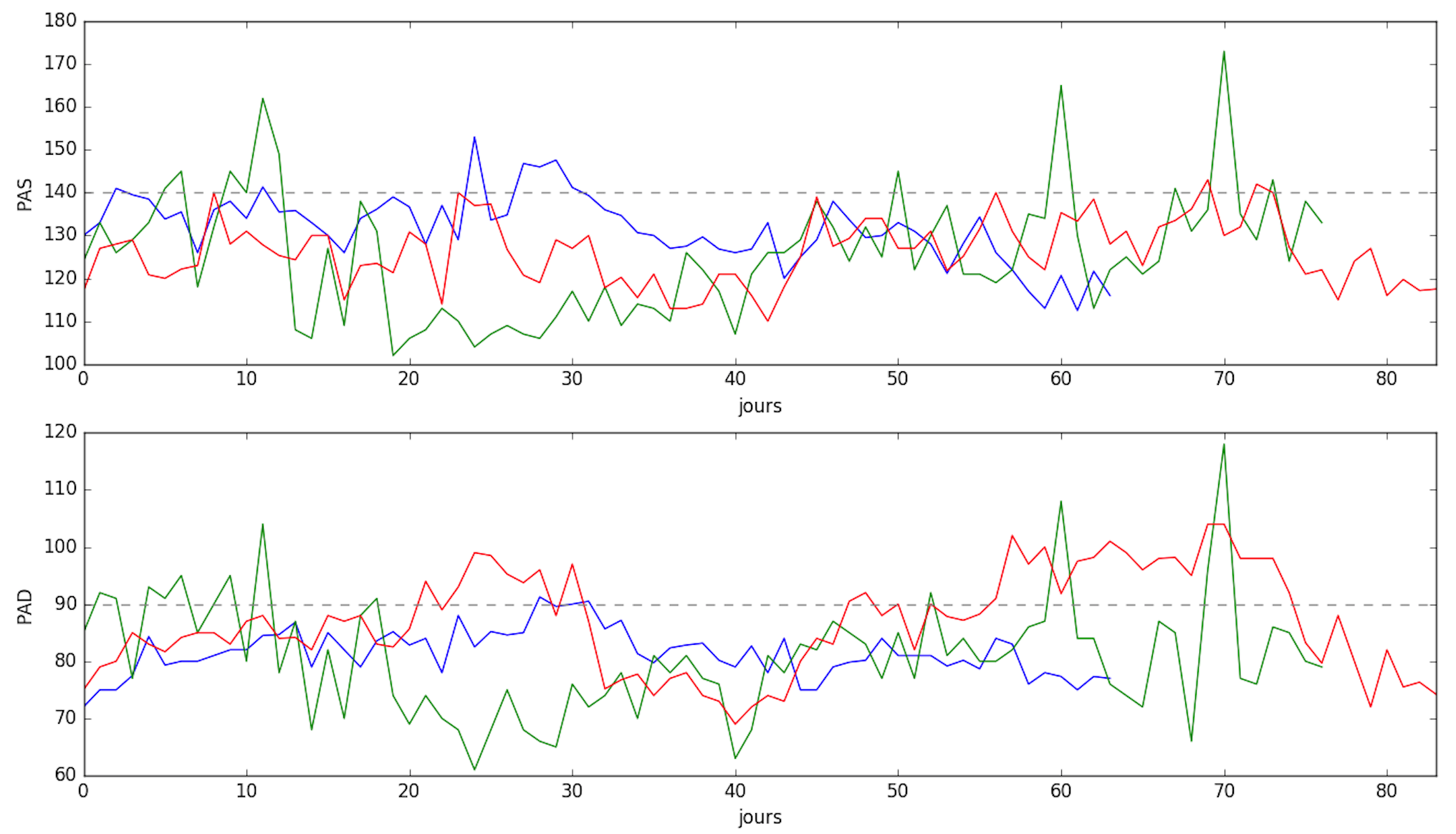
Suite à cette analyse de la première phase de traitement nous pourrions définir la stratégie de télé-monitoring suivante : tous les patients dont le taux de dépassement en phase 1 est supérieur à 15% doivent continuer à être suivis par tensiomètre connecté, il est de même pour les patients qui ne respectent pas le profil de la première phase du traitement. Cet algorithm d'aide à la décision nous a permis donc d'éliminer 6 patients du processus de télé-monitoring.